1. This answer is ambiguous because the statement is ambiguous. GDP is a measure of the total dollar amount of production which takes place in an economy during a year. Total goods and services sold will differ from total goods and services produced for two reasons: (1) some of the goods sold were produced in previous years, and (2) some of the goods produced in a year are sold in subsequent years. For this reason, given sales, we need to add end of the year inventories and subtract start of the year inventories . Given this, some students say that the statement is false, because it should say the value of the net change in inventories. Others say that it is true but incomplete, since it is true that you have to add end of the year inventories. Still others say that it is uncertain, because the statement does not specify that it is talking about, end of the year or start of the year inventories.
2. a. To solve for the equilibrium value of Y, one has to set Y equal to total expenditures, Z, and solve for Y. In the model given in this question, Z is given by:
b. Disposable income is given by YD = Y - T = 3400 - 400
= 3000
c. Private savings is given by S = YD - C = 3400 - 400 -
[400 +.75 (3400 - 400)]
3400 - 400 - 2650 = 350
3. a. To answer this question redo part a of the previous question substituting 550 for the 450. The result is:
Y = 400 + .75 (Y - 500) + 450 + 400
[Note: The result in part c illustrates what is called the balanced budget multiplier. In this model an equal increase in taxes and government expenditures expands the economy. The effect of an increase in taxes to decrease income is not as strong as the effect of an equal increase in government expenditures to increase income. Be sure you know why this is the case.]
4. a. Use the same method to solve this problem. This time instead of being constant, taxes depend upon income.
5 a. Again we have to add the new expression to the model and solve for equilibrium income.
b. S = YD - C = 3000 - 400 - [300 +.75 (3000-400)] = 2600
- 2250 = 350
Savings is no different than it was in the previous model (see 2 part
c)
c. I will give two explanations. This result is sometimes called the paradox of thrift. The reduction in the consumption function - from C = 400 + .75 YD to C = 300 + .75 YD represents an increase in the savings function (from S = -400 + .25 YD to S = -300 + .25 YD). This increased desire to save leads to a decrease in equilibrium GDP, and therefore savings doesn't actually go up. The act of trying to save more winds up defeating itself.
Another way to look at this is to express the equilibrium condition not as Z=Y, but as its equivalent in terms of savings and investment. Start with
Y = C + I + G.
Subtract taxes from both sides of the equation, yielding
Y - T = C + I + G - T.
Subtract consumption from both sides of the equation, yielding
Y - T - C = S = I + G - T.
This equation tells us that S will equal I + G - T, and since the change in c0 does not change I, G, or T, there can be no change in S.]
Y - c1 Y = c0 - c1 T + I0 + G0
(1 - c1) Y = c0 - c1 T + I0 + G0
Y = 1/(1 - c1) [c0 - c1 T + I0 + G0]
[Note: This is the basic multiplier equation.]
Y - c1 Y = c0 - c1 T - c1 X+ I0 + G0 + X
(1 - c1) Y = c0 - c1 T + I0 + G0 + (1 - c1) X
Y = 1/(1 - c1) [c0 - c1 T + I0 + G0 + (1 - c1) X]
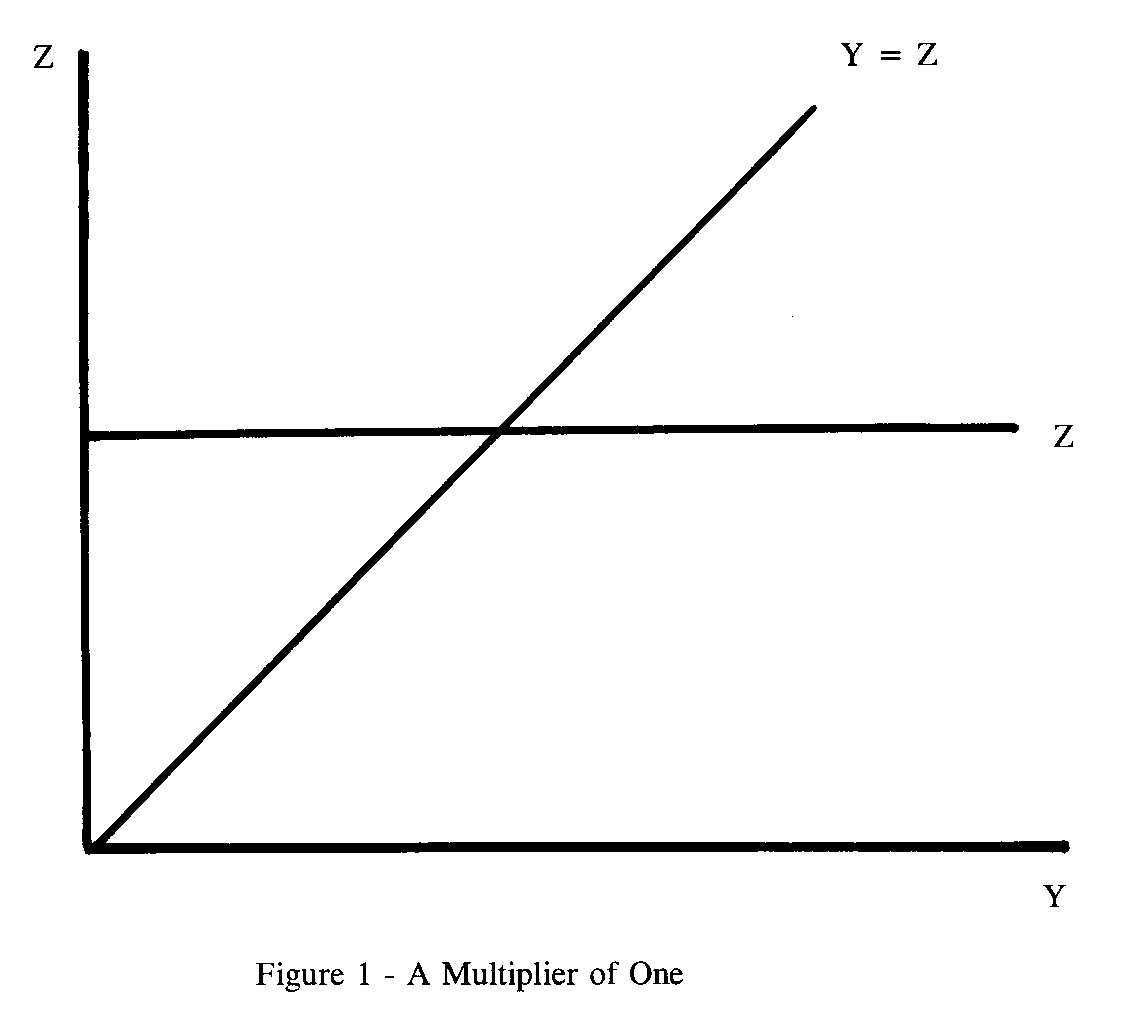
8. Figure 1 gives the answer. Since the multiplier is 1/(1-c1), it equals 1 if c1 equals zero. This leads to a horizontal total expenditure function.

9. a. We can use the same approach on this more complicated model.
Y - c1 Y + m Y = c0 - c1 T + I0 + G0 + X0 - q0
(1 - c1 + m) Y = c0 - c1 T + I0 + G0 + X0 - q0
Y = 1/(1 - c1 + m) [c0 - c1 T + I0 + G0 + X0 - q0]
c. The multiplier would be 1/(1 - c1 + m)
1/(1- c1 + m) = 1/(1 - .75 + .2) = 1/.45 = 2.22
The logic behind this result is that imports are income earned by individuals in other countries, hence spending on imports does not represent new income for those in the home country. When we ignore imports we ignore a leakage from the economy and as a result have a larger multiplier.